
Acerca de
Content Knowledge
Unit Lesson Plan
Download the lesson plans for references.
The lesson plans linked below detail the instructional direction for GSE Pre-Calculus, Unit 5. This unit contains focus standards in which students explore the basics of matrix characteristics and operations and support standards in which students connect their knowledge on matrices to the concept of vectors.
For more information about the content standards and expectations, see the documents below, originally found on georgiastandards.org.
Another highlight of my GSE Pre-Calculus curriculum includes the project students completed in Unit 2, wherein they studied the legal guidelines for wheelchair ramps codified in the Americans with Disabilities Act. After calculating the incline in degrees using inverse trigonometry, students found locations around the school's campus that could benefit from the construction of a wheelchair ramp. Students calculated the dimensions and 3D printed a scale model of their design. See artifacts from this project below.


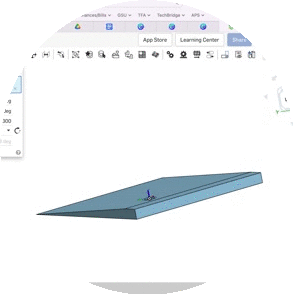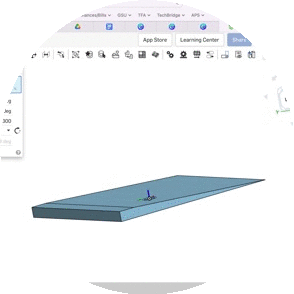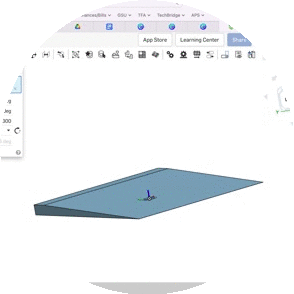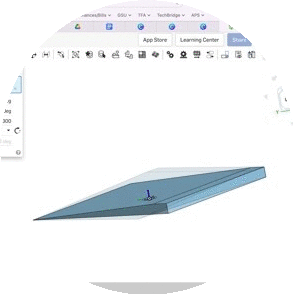
Sample Mathematics Coursework
Below are two samples of work that I have submitted for various masters-level mathematics courses. Sample 1 is a homework assignment for College Geometry, in which I designed geometric constructions in GeoGebra and proved their findings. This assignment received a 100%. Sample 2 is my submission for the second of four exams administered in the summer course, "Bridge to Higher Mathematics." Proving methods and set theory were at the heart of this course's content, and the exam below earned a 96%. The professors of both of these courses have approved of this material appearing on my Digital Dossier.
Content Knowledge Reflection
I earned my undergraduate degree in Business Administration, with a focus in Strategy & Innovation, at Georgia Tech in 2020. Having a background in a STEM-adjacent field, I believe, has enhanced my ability to be an effective math educator. By taking graduate-level mathematics courses after four years of business courses, I have a thorough understanding of both the underlying theory of math and math education, as well as a broad set of tangible applications for those math concepts that influence my teaching. Additionally, I bring a lens that is attuned student misconceptions because sometimes they are misconceptions that I carried at some point during my math career.
One way that I expand my instructional capacity is through my integration of Excel and Google Sheets in the classroom, about which I have an extensive understanding from previous jobs and coursework. Many different fields utilize these programs to perform mathematical analyses instead of, or in addition to, the use of scientific or graphing calculators. So, in addition to teaching students how to calculate compounded and discounted values when teaching standard MGSE9-12.A.CED.2 – creating exponential equations in two or more variables – I also teach students how to input the same information into a future value or present value formula in Excel. I use similar techniques to teach standards in statistics, linear algebra, and trigonometry. This allows students to extend their conceptual understanding of a new concept even if their prerequisite procedural fluency is not up to par. Students also walk away with the advantage of understanding the basics of a widely used program and have a broad understanding of how it can aid them in solving future problems in a variety of contexts.
My approach to addressing student misconceptions begins during the planning process. When I unpack a standard and choose my tasks and assessments, I also anticipate the common mistakes students might make. The first strategy I employ is mitigation: I strive to teach the concept initially by using precise language, repetition, and small steps. This often occurs in the form of a Think Aloud, in which I can verbally express the process of redirecting a potential misconception. Then, while monitoring individual student progress, I use probing questions so students can explain the logic behind their thinking. If many students are experiencing the same misconception, I take the opportunity to reteach. For example, many students consistently make miscalculations when multiplying fractions. A common phrase I’ve repeated throughout the year is, “numerator times numerator over denominator times denominator.” If a student makes a mistake in a problem that involves multiplying fractions, I can ask, “what individual calculations did you make to achieve your answer?” Then, while reviewing answers to problems as a whole group, I can address the multiple correct and incorrect methods I observed and engage students in fixing those mistakes.
My goal over the course of my teaching career is to continue to find relevant and innovative applications for the math standards I teach and become a better predicter of student responses. This will allow my lessons to contain student-driven segues and exemplify teaching strategies that are effective at engaging students and helping them commit more topics to memory.